Geometria : Lembrete

Fórmulas para o cálculo de perímetros

O perímetro de uma figura fechada é definido como o comprimento de seu contorno.

Perímetro de um círculo

A fórmula para calcular o perímetro de um círculo `P=2*pi*r`, onde r é o raio do círculo.
Exemplo: o perímetro de um círculo de comprimento 1 é igual a 2*pi .

Perímetro de um retângulo

O perímetro de um retângulo é dado pela fórmula `2*(L+l)` onde L é o comprimento e l é a largura de um lado. Ao aplicar esta fórmula, é possível verificar que o perímetro de um retângulo de comprimento é 3 e largura 2 é igual a 10 .

Perímetro de um quadrado

O perímetro de um quadrado é dado pela fórmula `4*a` oonde a é o comprimento de um lado do quadrado. Usando esta fórmula, podemos mostrar que o perímetro de um quadrado de comprimento 2 é igual a 8 .

Perímetro de um triângulo

O perímetro de um triângulo é dado pela fórmula a+b+c onde a, b e c são o comprimento de cada lado do triângulo Usando esta fórmula, podemos ver que o perímetro de um triângulo com lados de comprimento 5, 6, 7 é 18 .

Fórmulas de área

Área de um círculo

A área de um círculo é dada pela fórmula `pi*r^2`, onde r é o raio do círculo.

Ao aplicar esta fórmula, é possível encontrar a área de um círculo de raio 3 .

Área de um retângulo

A área de um retângulo é igual ao produto de seus lados e é calculada usando a fórmula `(L*l)`, onde L é o comprimento e l é a largura de um lado. Usando esta fórmula, podemos verificar que o comprimento é 3 e a largura é 6 .

Área de uma praça

A área de um quadrado é dada pela fórmula `a^2` onde a é o comprimento de um lado do quadrado.

Usando esta fórmula, podemos, por exemplo, calcular a área de um quadrado cujo comprimento lateral é 3 .

Área de um triângulo

A área de um triângulo pode ser calculada usando a fórmula de Heron, que está escrita: `S=sqrt(p*(p-a)*(p-b)*(p-c)`, onde a, b, c são os comprimentos dos lados do triângulo, e p é o meio perímetro `p=(a+b+c)/2`.

Usando esta fórmula, podemos, por exemplo, calcular a área de um triângulo cujos comprimentos laterais são 3, 4 e 5, respectivamente .

Fórmulas para o cálculo de volumes

Volume de uma esfera (bola)

O volume de uma esfera é dado pela fórmula `4/3*pi*r^3`, onde r representa o raio da esfera. Esta fórmula permite, por exemplo, calcular o volume de uma esfera de raio 3.

Volume de um paralelepípedo retangular

O volume de um paralelepípedo retangular é dado pela fórmula `(L*l*h)`, onde L é o comprimento, l é a largura de um lado e h é a altura. Usando esta fórmula, podemos calcular o volume de um paralelepípedo retangular cujo comprimento é 3, largura é 2, e altura é 4.

Volume de um cubo

O volume de um cubo é dado pela fórmula `l^3`, onde l é o comprimento de um lado. Ao aplicar esta fórmula, é possível encontrar o volume de um cubo que tem lados de comprimento 3.

Teorema de Pitágoras

O teorema de Pitágoras é declarado da seguinte forma : Em um triângulo em ângulo reto, o quadrado da hipotenusa é igual à soma dos quadrados dos lados opostos. Se considerarmos o triângulo ABC retangular em A, se colocarmos BC=a, AC=b, AB=c então o teorema de Pitágoras é escrito `BC^2=AB^2+AC^2` ou `a^2=b^2+c^2`.

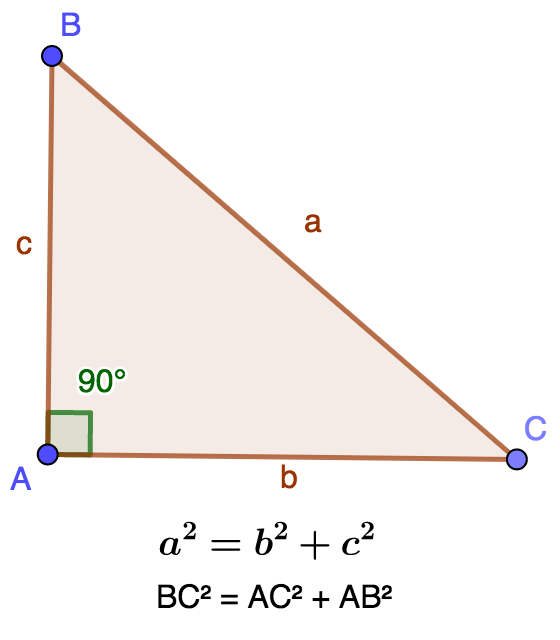
O teorema de Pitágoras tem uma reciprocidade que é declarada como segue: Se em um triângulo o quadrado de um lado for igual à soma dos quadrados dos lados opostos, então o triângulo é retangular.

Aplicando o teorema de Pitágoras, é possível, por exemplo, calcular o comprimento da hipotenusa de um triângulo em ângulo reto cujos lados adjacentes têm comprimentos de 3 e 4.